O mais numérico e estatístico dentro os meus hobbies é jogar RPG de mesa, já que uma característica bastante comum é usar a sorte para determinar o resultado do que acontece e a sorte nestes jogos é representada muitas vezes pelo rolar dos dados. Claro, o tipo, a quantidade e os modificadores aplicados aos dados são determinados por escolhas durante o jogo, assim como por fatores externos ao personagem e que pertencem a história que está sendo contada e ao sistema de regras utilizado.
O RPG mais conhecido é o Dungeons & Dragons, ele utiliza 6 diferentes tipos de dados, entre eles os sólidos platónicos com 4, 6, 8, 12 e 20 lados e uma abominação com 10 lados que só a imaginação de um herege poderia produzir. Como é perfeitamente visível na imagem, os dados são todos numerados e, portanto, a cada lançamento individual é obtido um resultado entre 1 o número de lados que o dado possui.

Em situações perfeitas, em que os dados não possuam irregularidades e sejam “justos”, ao se lançar um único dado uma quantidade de vezes tendendo ao infinito, é esperado que a frequência obtida seja uniforme, ou seja, cada valor possua a mesma frequência. O lançamento de um único dado — na notação mais comum 1ds — é um pouco tedioso, resultando somente em uma linha reta e uniforme entre os valores de 1 a N (sendo N o número de lados do dado).
Ao se lançar múltiplos dados, com o mesmo número de lados ou não, a soma dos resultados se aproxima a uma distribuição normal. Esse é um resultado muito mais interessante, mas pessoas comuns não são geralmente capazes de determinar as probabilidades de cada resultado rapidamente. Existe uma ferramenta online que facilita e muito a vida de quem deseja obter esses resultados, o AnyDice. Ela aceita um superset da notação para o lançamento de dados e fornece alguns gráficos e tabelas com os resultados.
Tudo isso é muito legal e interessante, mas é um pouco chato depender de uma ferramenta externa e não compreender os mecanismos que permitem gerar o resultado que ela fornece. Então eu decidi esboçar um pedaço de código para reproduzir o funcionamento do AnyDice, ao menos parcialmente.
Modelo de Dados
Nos últimos anos eu tomei gosto por iniciar um projeto sempre criando algumas estruturas que me permitam organizar o código e dar significado as variáveis que utilizo. Então minha primeira pergunta ao criar esse projeto foi: Qual a principal partícula de informação que eu quero representar? Minha escolha foi representar o conjunto composto por um valor arbitrário e a sua probabilidade de ocorrer.
class ValueProbability(NamedTuple):
"""
A named tuple to represent a value and its associated probability.
"""
value: int
probability: Fraction
def __str__(self):
return f"Value: {self.value}, Probability: {self.probability:.2%}"
def __repr__(self):
return f"ValueProbability(value={self.value}, probability={self.probability})"
No Python existem muitas formas de representar uma classe de dados — para uma visão mais ampla sobre o assunto, recomendo esse capítulo do livro Fluent Python — e eu escolhi usar a NamedTuple, com os campos value e probability. Para reduzir os erros gerados por arredondamento, decidi utilizar a classe Fraction para representar a probabilidade, pois ela armazena o numerador e o denominador separadamente.
Outro ponto presente nessa classe são os métodos __str__ e __repr__, eles estão entre os métodos mágicos do Python e uma introdução a eles pode ser encontrada aqui. Muitos métodos mágicos são utilizados nesse projeto, em especial para definir como as operações matemáticas se comportam.
Um único dado
Um único dado é tedioso, e por causa disso mais simples de modelar e implementar. O cálculo da distribuição é extremamente simples, para cada valor presente no dado, a probabilidade dele ocorrer é 1/s, onde s é o número de lados do dado. Uma adição importante é o offset, conhecido como modificador, que é um número somado ao resultado da jogada. A notação adotada para representar a jogada de um dado de 6 lados com um modificador/offset de 3 é 1d6+3.
class Die:
def __init__(self, sides: int = 6, offset: int = 0):
if sides < 1 or not isinstance(sides, int):
raise ValueError("Number of sides must be a positive integer.")
self._sides = sides
self._offset = offset
@property
def sides(self):
return self._sides
@property
def offset(self):
return self._offset
def min_range(self):
"""
Returns the minimum value of the die.
"""
start = 1
return start + self.offset
def max_range(self):
"""
Returns the maximum value of the die.
"""
end = self.sides
return end + self.offset
def range(self):
"""
Returns an iterator over the sides of the die.
"""
start = self.min_range()
end = self.max_range()
return iter(range(start, end + 1))
def distribution(self):
"""
Returns a list of the possible outcomes of rolling the die.
"""
return [ValueProbability(i, Fraction(1, self.sides)) for i in self.range()]
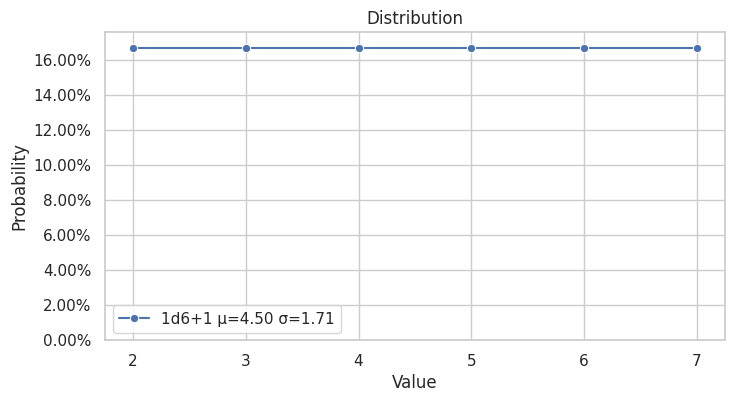
Essa classe possui os métodos min_range, max_range, range e distribution e eles são os responsáveis pelo cálculo da distribuição do dado, que é uma lista de ValueProbability:
ValueProbability(value=2, probability=1/6)
ValueProbability(value=3, probability=1/6)
ValueProbability(value=4, probability=1/6)
ValueProbability(value=5, probability=1/6)
ValueProbability(value=6, probability=1/6)
ValueProbability(value=7, probability=1/6)
Uma função foi criada para plotar a distribuição, com o seguinte resultado:
Um ponto importante a se notar no código é o uso do decorador @property, além de permitir que um método seja chamado como se fosse um atributo, ele acaba por criar proteções a modificação da instância da classe não intencionais. Isso vai ser útil quando quisermos criar uma nova instância a partir de uma já existente, impedindo alguns bugs que poderiam ocorrer caso o estado da instância fosse alterado e ela fosse referenciada por múltiplas variáveis. Python é uma linguagem que privilegia a liberdade do programador de fazer o que bem entender, então muitas vezes a adição de barreiras a essa liberdade é útil. Claro, caso alguém queira modificar o estado interno da instância, é só acessar o atributo diretamente, mas isso deve ser feito de forma consciente e intencional.
Múltiplos dados
A segunda pergunta importante que eu fiz foi: Agora que eu tenho como representar um único dado, como eu represento a distribuição de múltiplos dados? A resposta é provavelmente depende, eu optei por criar uma classe Dice que possui uma lista de Die e um offset. A primeira coisa que eu fiz foi criar um algoritmo para calcular a distribuição do conjunto de dados a partir da distribuição de cada dado, obviamente minha primeira solução foi um fracasso em termos de performance.
Fazer o produto cartesiano parece funcional para até uma dezena de dados, mas se torna extremamente ineficiente quando se busca algo mais complexo. Para causar vergonha alheia a todos os que lerem esse código, o algoritmo ainda está presente no método distribution_brute_force. Após esbarrar nesse problema de desempenho, eu comecei a procurar formas mais eficientes de calcular a distribuição, uma das soluções parece envolver a Transformada Rápida de Fourier, enquanto a outra era mais simples e envolvia a convolução entre as distribuições de cada dado e é implementada no método distribution.
class Dice:
def __init__(self, *dice: Die, offset: int = 0):
self._dice: tuple[Die, ...] = dice
self._offset: int = offset
@property
def offset(self):
return self._offset
@property
def dice(self):
return self._dice
def range(self):
"""
Returns an iterator over the possible outcomes of rolling the combined dice.
"""
start_value = sum(die.min_range() for die in self.dice) + self.offset
end_value = sum(die.max_range() for die in self.dice) + self.offset
return iter(range(start_value, end_value + 1))
def distribution_brute_force(self):
"""
Returns the distribution of the combined dice.
"""
start_time = time.time()
combined_distribution: list[ValueProbability] = []
dists = [die.distribution() for die in self.dice]
print(f"Time to create distributions: {time.time() - start_time:.2f} seconds")
i = 0
for dice in product(*dists):
# Calculate the sum of the values and the product of the probabilities
value = sum(vp.value for vp in dice)
probability = 1
for vp in dice:
probability *= vp.probability
vp = ValueProbability(value, probability)
combined_distribution.append(vp)
i += 1
print(i)
print(
f"Time to create combined distribution: {time.time() - start_time:.2f} seconds"
)
# Combine the distributions
combined_distribution_dict: defaultdict[int, Fraction] = defaultdict(
lambda: Fraction(0)
)
for vp in combined_distribution:
combined_distribution_dict[vp.value] += vp.probability
combined_distribution = [
ValueProbability(value + self.offset, probability)
for value, probability in combined_distribution_dict.items()
]
print(f"Time to combine distributions: {time.time() - start_time:.2f} seconds")
return sorted(combined_distribution, key=lambda vp: vp.value)
@staticmethod
def conv(a: list[ValueProbability], b: list[ValueProbability]):
c = defaultdict(lambda: Fraction(0))
for va, pa in a:
for vb, pb in b:
c[va + vb] += pa * pb
return [ValueProbability(v, p) for v, p in c.items()]
def distribution(self):
"""
Returns the distribution of the combined dice using convolution.
"""
dist = [ValueProbability(0, Fraction(1))]
for die in self.dice:
base = die.distribution()
dist = self.conv(dist, base)
return [
ValueProbability(value + self.offset, probability)
for value, probability in dist
]
Usando a Convolução para 2 dados
Supunhetemos que queremos a distribuição de 1d6+1d4, sabemos que a distribuição de 1d6 é:
ValueProbability(value=1, probability=1/6)
ValueProbability(value=2, probability=1/6)
ValueProbability(value=3, probability=1/6)
ValueProbability(value=4, probability=1/6)
ValueProbability(value=5, probability=1/6)
ValueProbability(value=6, probability=1/6)
E a distribuição de 1d4 é:
ValueProbability(value=1, probability=1/4)
ValueProbability(value=2, probability=1/4)
ValueProbability(value=3, probability=1/4)
ValueProbability(value=4, probability=1/4)
Começamos pegando ValueProbability(1, 1/6): O valor 1 será somado aos valores 1, 2, 3 e 4 presentes na distribuição de 1d4, e a probabilidade 1/6 será multiplicada por 1/4, resultando em 1/24. O resultado dessa operação é:
ValueProbability(2, 1/24)
ValueProbability(3, 1/24)
ValueProbability(4, 1/24)
ValueProbability(5, 1/24)
Repetimos esse processo para ValueProbability(2, 1/6), o valor 2 será somado aos valores 1, 2, 3 e 4 presentes na distribuição de 1d4, e a probabilidade 1/6 será multiplicada por 1/4, resultando em 1/24. O resultado dessa operação é:
ValueProbability(3, 1/24)
ValueProbability(4, 1/24)
ValueProbability(5, 1/24)
ValueProbability(6, 1/24)
Sendo a concatenação dos dois resultados:
ValueProbability(2, 1/24)
ValueProbability(3, 1/24)
ValueProbability(4, 1/24)
ValueProbability(5, 1/24)
ValueProbability(3, 1/24)
ValueProbability(4, 1/24)
ValueProbability(5, 1/24)
ValueProbability(6, 1/24)
Alguns valores se repetem, para simplificar somamos as probabilidades destes valores, resultando em:
ValueProbability(2, 1/24)
ValueProbability(3, 2/24)
ValueProbability(4, 2/24)
ValueProbability(5, 2/24)
ValueProbability(6, 1/24)
Esse processo continua até chegarmos a ValueProbability(6, 1/6), em que teremos como resultado final:
ValueProbability(value=2, probability=1/24)
ValueProbability(value=3, probability=1/12)
ValueProbability(value=4, probability=1/8)
ValueProbability(value=5, probability=1/6)
ValueProbability(value=6, probability=1/6)
ValueProbability(value=7, probability=1/6)
ValueProbability(value=8, probability=1/8)
ValueProbability(value=9, probability=1/12)
ValueProbability(value=10, probability=1/24)
O plot dessa distribuição é:

Convolução para 3+ dados
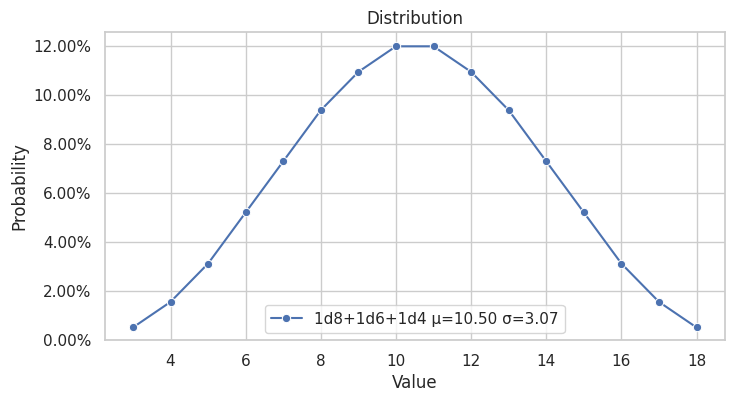
Agora queremos adicionar um dado a mais a nossa distribuição, por exemplo 1d6+1d4+1d8. A distribuição de 1d8 é:
ValueProbability(value=1, probability=1/8)
ValueProbability(value=2, probability=1/8)
ValueProbability(value=3, probability=1/8)
ValueProbability(value=4, probability=1/8)
ValueProbability(value=5, probability=1/8)
ValueProbability(value=6, probability=1/8)
ValueProbability(value=7, probability=1/8)
ValueProbability(value=8, probability=1/8)
O segredo é iniciarmos com a distribuição que já possuímos (1d6+1d4) e repetirmos o processo de convolução com a distribuição de 1d8, para termos esse belo gráfico:
Mais detalhes sobre convolução
O meu divulgador matemático favorito é o Grant Sanderson, então vou deixar aqui esse vídeo dele explicando o que é convolução:
Adicionando operações
Existem duas classes de operações que queremos representar nesse projeto: números inteiros e Die | Dice; Die | Dice e Die | Dice. Para ambas utilizei os métodos mágicos, citados anteriormente. O uso deles permite fazer o overloading de operadores, como +, * e @. Eu não vou me estender a explicar todos os métodos mágicos utilizados, visto que muitos recaem no uso de outro método mágico, por exemplo a subtração pode ser vista como a adição de um número negativo.
Multiplicação
Na classe Die foi adicionado a propriedade weight para representar a multiplicação do dado por um número inteiro. Pegamos por exemplo 2*1d6 — diferente de 2d6 — e vejamos como essa operação modifica a distribuição.
Antes:
ValueProbability(1, 1/6)
ValueProbability(2, 1/6)
ValueProbability(3, 1/6)
ValueProbability(4, 1/6)
ValueProbability(5, 1/6)
ValueProbability(6, 1/6)
O resultado é uma distribuição em que os valores foram multiplicados por 2, mas as probabilidades continuam as mesmas:
ValueProbability(2, 1/6)
ValueProbability(4, 1/6)
ValueProbability(6, 1/6)
ValueProbability(8, 1/6)
ValueProbability(10, 1/6)
ValueProbability(12, 1/6)
A implementação do método __mul__ tem também que lidar com o offset:
def __mul__(self, weight: int):
if weight == 0:
return 0
if isinstance(weight, int):
return Die(self.sides, self.offset * weight, self.weight * weight)
raise TypeError(
"Unsupported operand type(s) for *: 'Die' and '{}'".format(
type(weight).__name__
)
)
def min_range(self):
"""
Returns the minimum value of the die.
"""
start = 1
if self.weight < 0:
start = self.sides
return start * self.weight + self.offset
def max_range(self):
"""
Returns the maximum value of the die.
"""
end = 1
if self.weight > 0:
end = self.sides
return end * self.weight + self.offset
def range(self):
"""
Returns an iterator over the sides of the die.
"""
start = self.min_range()
end = self.max_range()
return iter(range(start, end + 1, abs(self.weight)))
No caso da classe Dice, o processo é feito através da criação de execução do método __mul__ por meio do operador * para cada item presente em self.dice, sendo então retornada uma nova instância de Dice. O offset presente também é multiplicado pelo número inteiro.
def __mul__(self, weight: int):
if weight == 0:
return 0
if isinstance(weight, int):
dice = tuple(die * weight for die in self.dice)
offset = self.offset * weight
return type(self)(*dice, offset=offset)
raise TypeError(
"Unsupported operand type(s) for *: 'Dice' and '{}'".format(
type(weight).__name__
)
)
Multiplicação Matricial
Após implementar a multiplicação convencional, o operador * ficou indisponível para representar a quantidade de dados lançados. Como o Python adicionou o operador @ para representar a multiplicação matricial na biblioteca numpy, minha escolha obvia se tornou usar ele para representar esse outro tipo de multiplicação. Por causa disso, a notação 2d6 se traduz ao utilizar esse código em 2@Die(6) e gera uma instância de Dice com 2 dados de 6 lados internamente.
A implementação desse método foi feita tanto na classe Die conforme o código abaixo, em que ao se utilizar o operador @ — representado pelo método mágico __matmul__ — junto a uma instância de Die, o resultado é pegar essa instância e criar N novas instâncias de Die que possuam as mesmas características. N também pode ser um número negativo, nesse caso o sinal do offset e do weight são invertidos.
def __matmul__(self, other: int):
if isinstance(other, int) and other >= 0:
dice = tuple(
Die(self.sides, self.offset, self.weight) for _ in range(other)
)
return Dice(*dice)
if isinstance(other, int) and other < 0:
dice = tuple(
Die(self.sides, -self.offset, -self.weight) for _ in range(-other)
)
return Dice(*dice)
raise TypeError(
"Unsupported operand type(s) for *: 'Die' and '{}'".format(
type(other).__name__
)
)
O caso da classe Dice é uma expansão desse conceito, para cada Die interno a classe, eu crio N novas instâncias com as mesmas características. Por exemplo: 2 @ Dice(Die(6), Die(4)) é o equivalente a 2d6+2d4.
def __matmul__(self, other: int):
if isinstance(other, int) and other >= 0:
dice = tuple(
Die(die.sides, die.offset, die.weight) for die in self.dice * other
)
offset = self.offset * other
return type(self)(*dice, offset=offset)
if isinstance(other, int) and other < 0:
dice = tuple(
Die(die.sides, -die.offset, -die.weight)
for die in self.dice * abs(other)
)
offset = self.offset * other
return type(self)(*dice, offset=offset)
raise TypeError(
"Unsupported operand type(s) for *: 'Dice' and '{}'".format(
type(other).__name__
)
)
Adição
O processo de adição é ridiculamente simples. No caso de um inteiro, se adiciona o valor ao offset e no caso de Die | Dice, cria-se uma novo Dice cujo estado interno é composto pelos dois dados.
def __add__(self, other: Self | int):
if isinstance(other, int):
return Die(self.sides, self.offset + other, self.weight)
if isinstance(other, type(self)):
return Dice(self, other)
raise TypeError(
"Unsupported operand type(s) for +: 'Die' and '{}'".format(
type(other).__name__
)
)
Próximos passos
O próximo passo nesse projeto é criar um parser que receba a notação 1d6+1d4 e partir disso gere a distribuição esperada. Ainda não fiz, então fica para um futuro artigo. O código completo está disponível em Github.